Quadratic Reciprocity Law

The Reciprocity Law one

Let \(p\) and \(q\) be distinct odd prime numbers, and define the Legendre symbol as

\[\left({\frac{q}{p}}\right)= \begin{cases}1&{\text{if }}n^{2}\equiv q{\mod {p}}{\text{ for some integer }}n\\ -1&{\text{otherwise}} \end{cases}\] Then

\[\left(\frac {p}{q}\right)\left(\frac{q}{p}\right)=(-1)^{p^{\prime}q^{\prime}}.\]

where \(p^{\prime} = \frac{p-1}{2}\) and \(q^{\prime}=\frac{q-1}{2}\).

Since \(p^{\prime}q^{\prime}\) is even if either \(p\) or \(q\) is of the form \(4n+1\), and odd if both are of the form \(4n + 3\), we can also state the theorem as

The Reciprocity Law two

If \(p\) and \(q\) are odd primes, then \[\left(\frac {p}{q}\right) = \left(\frac{q}{p}\right)\] unless both \(p\) and \(q\) are of the forv \(4n+3\), in which case \[\left(\frac {p}{q}\right) = - \left(\frac{q}{p}\right)\]

The Reciprocity Lemma

If \[S(q,p) = \sum_{s=1}^{p^{\prime}}\left[\frac{sq}{p}\right],\] then \[S(q,p) + S(p,q) = p^{\prime}q^{\prime}.\]

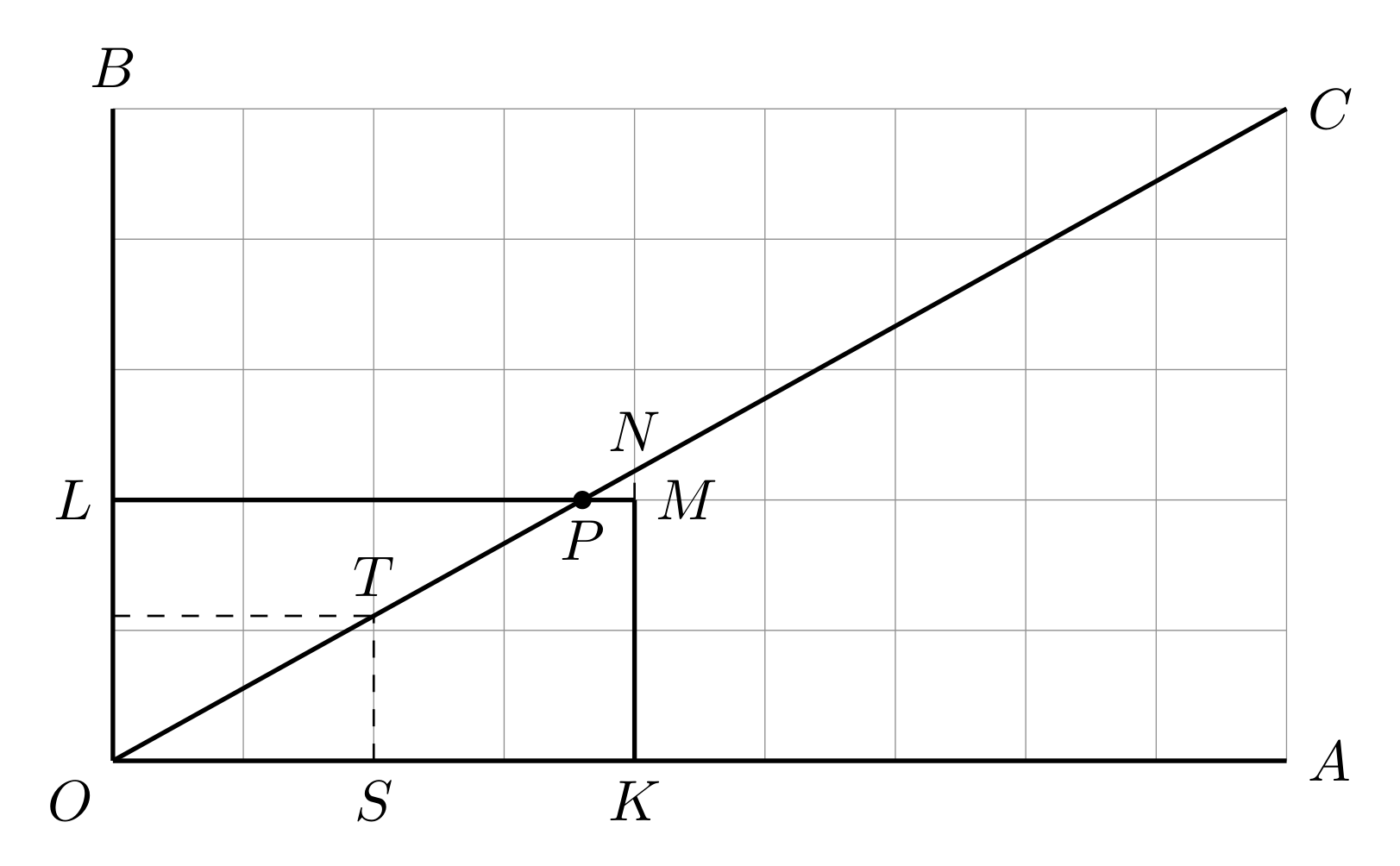
The proof may be stated in a geometrical form. In the figure \(AC\) and \(BC\) are \(x = p\), \(y=q\), and \(KM\) and \(LM\) are \(x = p^{\prime}\), \(y = q^{\prime}\). If (as in the figure) \(p > q\), then \(q^{\prime}/p^{\prime} < q/p\), and \(M\) falls below the diagonal \(OC\). Since \[q^{\prime} < \frac{qp^{\prime}}{p} < q^{\prime}-l,\] there is no integer between \(KM = q^{\prime}\) and \(KN = qp^{\prime}/p\).

We count up, in two different ways, the number of lattice points in the rectangle \(OKML\), counting the points on \(KM\) and \(LM\) but not those on the axes. In the first place, this number is plainly \(p^{\prime}q^{\prime}\). But there are no lattice points on \(OC\) (since \(p\) and \(q\) are prime), and none in the triangle \(PMN\) except perhaps on \(PM\). Hence the number of lattice points in \(OKML\) is the sum of those in the triangles \(OKN\) and \(OLP\) (counting those on \(KN\) and \(LP\) but not those on the axes). The number on \(ST\), the line \(x = s\), is \([sq/p]\), since \(sq/p\) is the ordinate of \(T\). Hence the number in \(OKN\) is \[\sum_{s=1}^{p^{\prime}}\left[\frac{sq}{p}\right] = S(q,p)\] Similarly, the number in \(OLP\) is \(S(p, q)\), and the conclusion follows.

The proof of Reciprocity Law

We can write \[\begin{equation} \label{eq: summing} kq = p \left[\frac{kq}{p}\right] + u_{k} \end{equation}\] where \(1\leq k \leq p^{\prime}\), \(1 \leq u_{k} \leq p-1\). Here \(u_k\) is the least positive residue of \(kq (\bmod \, p)\). If \(u_k = v_k \leq p^{\prime}\), then \(u_k\) is one of the minimal residues \(r_i\), while if \(u_k = w_k > p^{\prime}\), then \(u_k - p\) is one of the minimal residues \(-r^{\prime}_{j}\). Thus \[r_i = v_k, \quad r^{\prime}_{j} = p - w_k\] for every \(i,j\) and some \(k\).

The \(r_i\) and \(r_j^{\prime}\) are the numbers \(1,2,\dots,p^{\prime}\) in some order. Hence, if \[R = \sum r_i = \sum v_k, \quad R^{\prime} = \sum r_{j}^{\prime} = \sum (p - w_k) = up - \sum w_k\] (where \(\mu\) is the number of \(r_j^{\prime}\)), we have \[R+R^{\prime} = \sum_{\nu=1}^{p^{\prime}} \nu = \frac{1}{2}\frac{p-1}{2}\frac{p+1}{2} = \frac{p^2 -1}{8},\] and so \[\begin{equation} \label{eq: From} \mu p +\sum v_k - \sum w_k = \frac{1}{8}(p^2-1) \end{equation}\] On the other hand, summing \(\eqref{eq: summing}\) from \(k=1\) to \(k=p^{\prime}\), we have \[\begin{equation} \label{eq: and} \frac{1}{8} q (p^2-1) = p S(q,p) + \sum u_{k} = p S(q,p) + \sum v_{k} + \sum w_k. \end{equation}\] From \(\eqref{eq: From}\) and \(\eqref{eq: and}\) we deduce \[\begin{equation} \label{eq: of} \frac{1}{8} (p^2-1) (q-1) = pS(q,p) + 2\sum w_k - \mu p. \end{equation}\] Now \(q-1\) is even, and \(p^2 -1 \equiv 0 (\bmod 8)\); so that the left-hand side of \(\eqref{eq: of}\) is even, and also the second term on the right. Hence (since \(p\) is odd) \[S(q,p) \equiv \mu (\bmod 2),\] and therefore, by Gauss's lemma, \[\left(\frac {q}{p}\right) = (-1)^{\mu} = (-1)^{S(q,p)}.\] Finally, \[\left(\frac {q}{p}\right)\left(\frac {p}{q}\right) = (-1)^{S(q,p) + S(p,q)} = (-1)^{p^{\prime}q^{\prime}}\] by preceding lemma.

[1] Hardy G.H., Wright E.M. - An Introduction to the Theory of Numbers (1975)